[알고리즘] 부분합, 누적합 (Prefix Sum) 쉽게 알아보기(파이썬)

부분합, 누적합이라고 불리우는 배열의 일부 구간에 대한 합을 매우 빠르게 구할 수 있게 해주는 스킬이다.

N개의 원소로 이루어진 배열이 주어졌을 때 반복문을 통해 부분 배열의 합을 구하려면 O(N)이 걸리는데, 부분합을 이용하면 모든 부분합을 O(1)에 바로바로 구할 수 있다.

 

1차원 배열

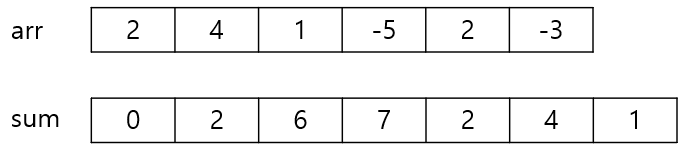
- 직관적으로 매우 쉽게 이해가 가능하다.  arr을 순차 탐색하면서 sum 배열을 만들어주면 된다.

sum[i]에는 arr[0] + arr[1] + ... + arr[i-1]의 정보가 담겨 있다고 생각하면 된다.

 

- 활용법

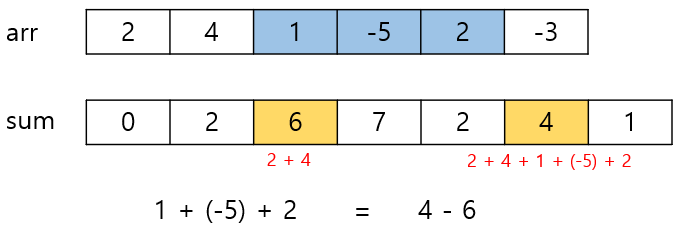
arr의 i항부터 j항까지의 합을 S(i, j)라고 하자.

이때 S(i, j) = sum[j+1] - sum[i]이다.

 

 

2차원 배열

- 2차원 배열도 같은 방식이다. arr을 순차 탐색하면서 sum 배열을 만들어주면 된다.

이때 sum[i][j]에는 arr[0][0]부터 arr[i-1][j-1]까지의 합이 담겨 있다고 생각하면 된다.

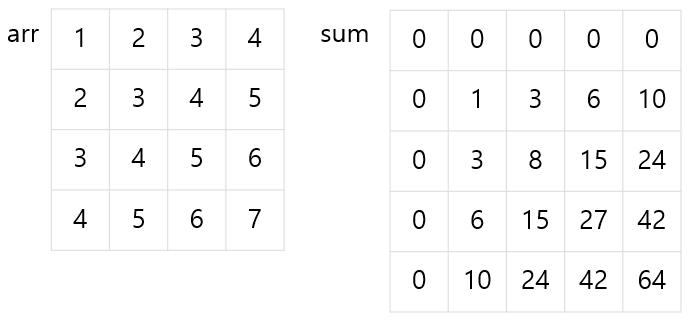
그림을 보면 바로 이해 가능

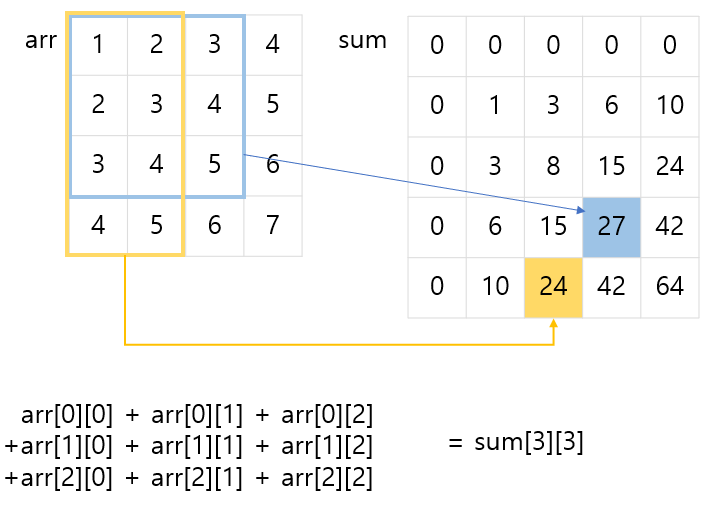
이때 그럼 sum 배열은 어떻게 만들지?? 아래와 같이 반복문 돌려주면 된다.

이때 기억해놓으면 좋은 식은 sum_arr[i][j] = arr[i-1][j-1] + sum_arr[i-1][j] + sum_arr[i][j-1] - sum_arr[i-1][j-1]

arr = [[1, 2, 3, 4],
       [2, 3, 4, 5],
       [3, 4, 5, 6]]

# 가로길이 4, 세로 길이 3
m = 4
n = 3

sum_arr = [[0 for _ in range(m+1)] for _ in range(n+1)]
for i in range(1, n+1):
    for j in range(1, m+1):
        sum_arr[i][j] = arr[i-1][j-1] + (sum_arr[i-1][j]) + (sum_arr[i][j-1]) - (sum_arr[i-1][j-1])

# 결과 보기
print('sum_arr : ')
for i in range(n+1):
    print(sum_arr[i])

그럼 예상한 결과가 잘 나온다.

sum_arr : 
[0, 0, 0, 0, 0]
[0, 1, 3, 6, 10]
[0, 3, 8, 15, 24]
[0, 6, 15, 27, 42]

 

 

- 2차원 구간합 활용법(중요!!)

이제 이 sum_arr을 활용하면 2차원 배열에서도 상수 시간에 구간합을 구할 수 있게 된다. 

arr의 (x1, y1)부터 (x2, y2)까지 합을 S라 할 때,

 S = sum[x2+1][y2+1] - sum[x1][y2+1] - sum[x2+1][y1] + sum[x1][y1]로 구할 수 있다.

 

 

 

 

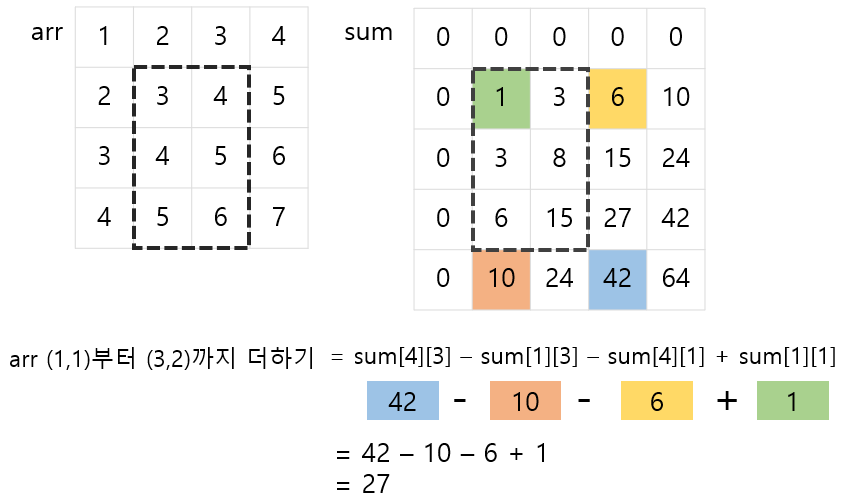
-진짜 진짜 활용(중요!)

이 문제를 풀어보자!

https://programmers.co.kr/learn/courses/30/lessons/92344

코딩테스트 연습 - 파괴되지 않은 건물