[누적합/파이썬] 백준 9527번 : 1의 개수 세기 / 골드 2

https://www.acmicpc.net/problem/9527

9527번: 1의 개수 세기

a, b = map(int, input().split())
psum = [0 for x in range(60)]

for i in range(1, 60):
    psum[i] = 2**(i-1) + 2 * psum[i-1]

def check(num):
    count = 0
    bin_num = bin(num)[2:]
    length = len(bin_num)

    for i in range(length):
        if bin_num[i] == '1':
            # pow : num 보다 크지 않으면서 가장 큰 2의 거듭제곱 수의 제곱 수
            pow = length-i-1
            # psum[pow] : num 보다 작은 자리수를 가진 수들의 1을 모두 카운트한 수
            count += psum[pow]
            # 가장 앞자리 1 개수를 세서 추가
            count += (num - 2 ** pow + 1)
            num = num - 2 ** pow
    return count

print(check(b) - check(a-1))

간단해 보이는 문제지만, 숫자 크기 제한 및 시간 제한으로 인해 무식한 방법으로는 절대 풀리지 않는 문제다.

 

1. 누적합 구하기

psum 배열을 먼저 구해준다. psum에는 2**n-1까지 등장하는 총 1의 개수를 담고있다.

psum[0] = 숫자 0까지 등장하는 1 개수(이진법 시) = 0

psum[1] = 숫자 1까지 등장하는 1 개수(이진법 시) = 1 = 2**0 + 2*0

psum[2] = 숫자 3까지 등장하는 1 개수(이진법 시) = 4 = 2**1 + 2*1

psum[3] = 숫자 7까지 등장하는 1 개수(이진법 시) = 12 = 2**2 + 2*4

psum[4] = 숫자 15까지 등장하는 1 개수(이진법 시) = 32 = 2**3 + 2*12

psum[5] = 숫자 31까지 등장하는 1 개수(이진법 시) = 80 = 2**4 + 2*32

 

이때 다음과 같은 점화식을 사용할 수 있다.

psum[i] = 2**(i-1) + 2 * psum[i-1]

 

 

 

2. 함수 정의하기

숫자 x를 인풋으로 받으면, 1부터 x까지 등장하는 1 개수를 리턴해주는 함수를 작성해보자. 이 함수를 f(x)라 하면

그럼 이 문제의 답은 f(b) - f(a-1)이 될 것이다. 

 

예시를 통해 방법을 구체화해보자.

x = 14일때,

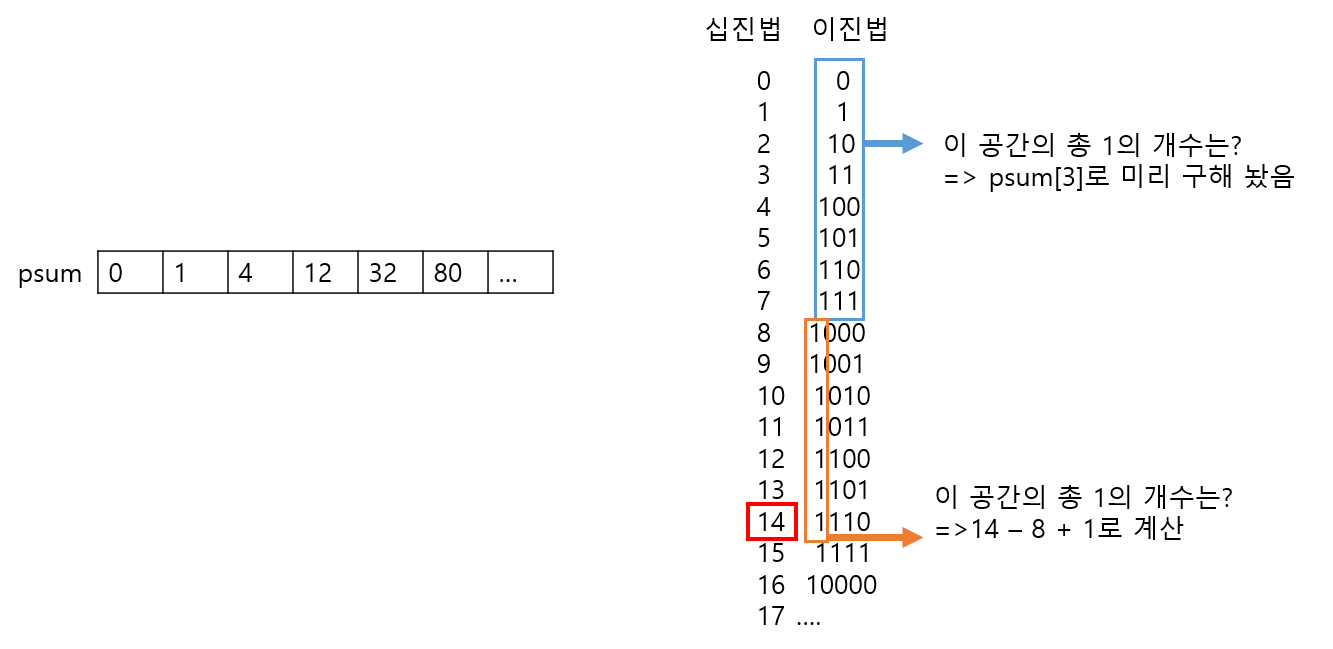
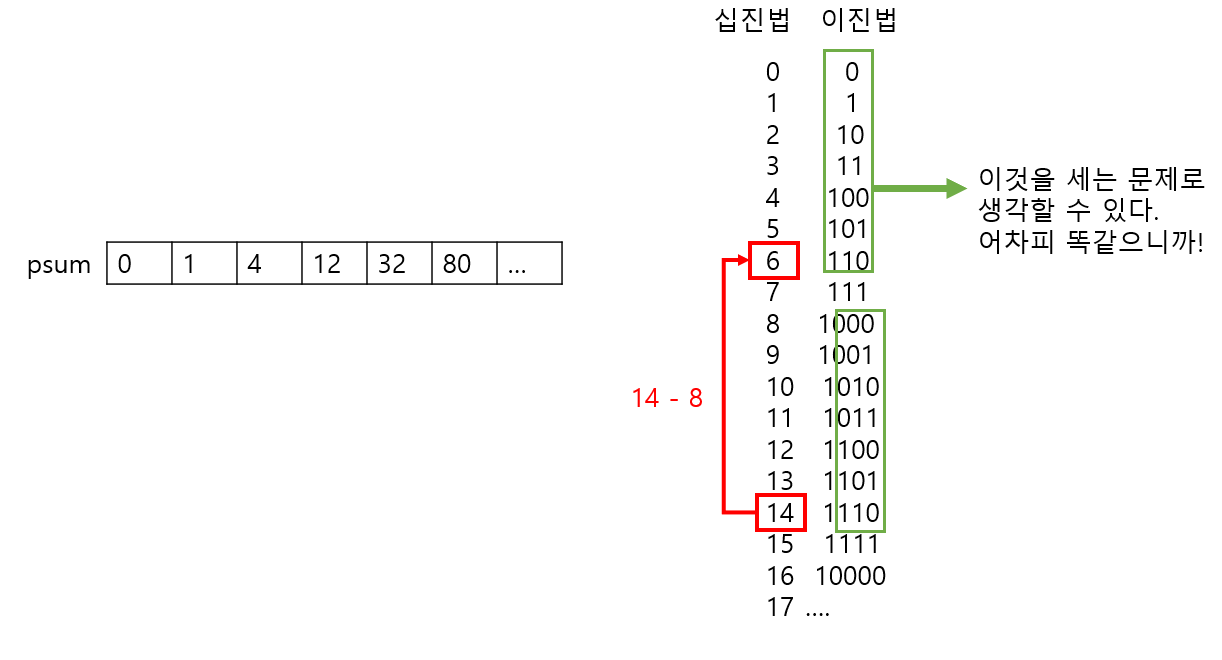
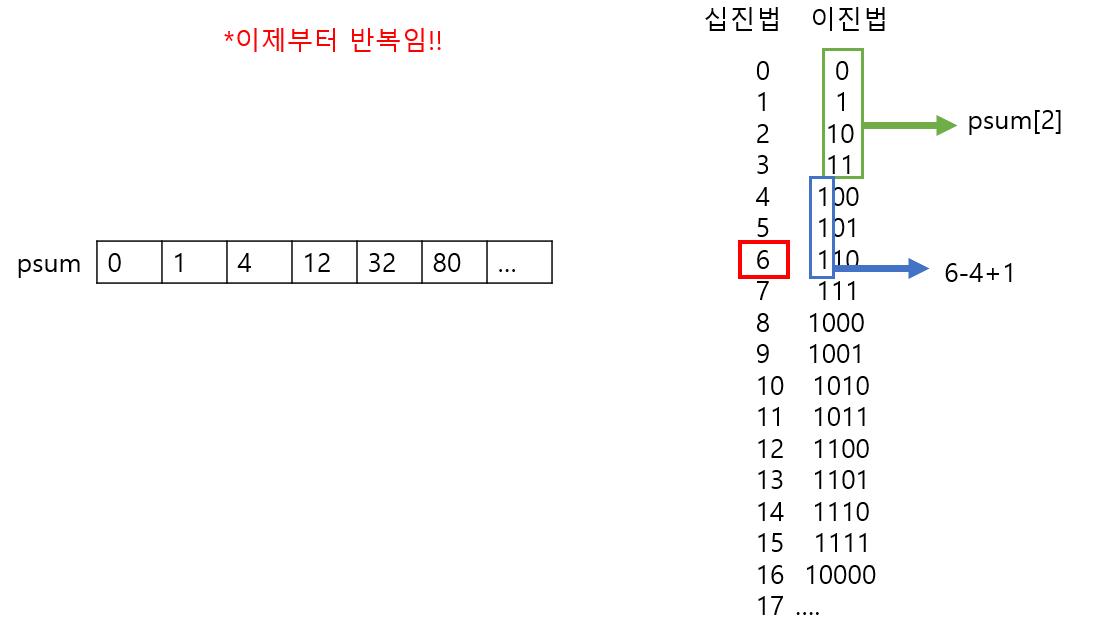
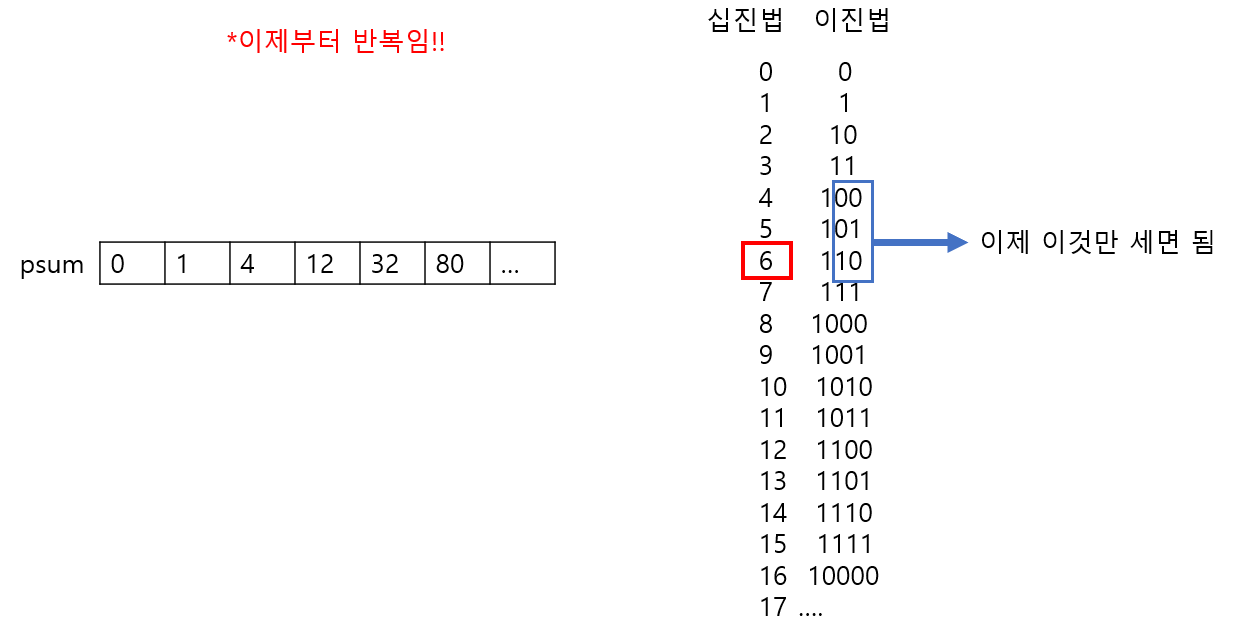
이해가 어려울 수 있지만, 어쨌든 위와 같은 구조로 결국 반복된다.

 

 

ps. 아직 너무 부족함을 느낀다. 너무 오래 걸린다..