그래프 알고리즘에는 대표적으로 다익스트라 알고리즘, 플로이드-워셜 알고리즘이 있다.
- 다익스트라 vs 플로이드-워셜
이 둘의 차이점은 다익스트라는 한 노드에서 다른 특정 노드까지의 최단 경로를 구할 때 사용되고,
플로이드-워셜은 모든 노드에서 다른 모든 노드까지의 최단 경로를 구할때 사용된다.
우선순위큐를 활용하여 구현한 다익스트라의 시간복잡도는 O(ElogV)이다. 이때 V는 노드의 개수, E는 간선의 개수이다.
반면 플로이드-워셜은 시간복잡도가 O(n3)이다. n번의 탐색동안 n2번 값을 비교하여 업데이트해준다.
또한 다익스트라는 그리디 알고리즘인데 플로이드-워셜은 다이나믹 프로그래밍이라는 특징이 존재한다.
- 플로이드-워셜 알고리즘의 개념
플로이드- 워셜의 결과는 항상 2차원 배열이다. 모든 노드에서 모든 노드로 가는 최단 경로가 모두 포함된 테이블이 형성되기 때문이다.
우선 초기 2차원 배열, 즉 테이블을 설정한다. 이때 본인 노드에서 본인 노드로 오는 경우는 당연히 거리가 0이 되고, 또 직접적으로 이어지지 않은 경로에 대해선 일단 임의의 큰 값을 집어 넣는다.
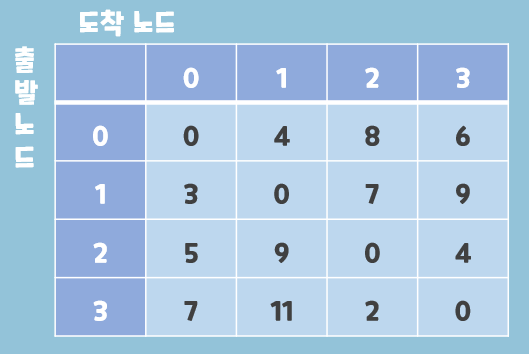
아래 그래프 예시를 보면 테이블은 다음과 같이 형성된다.


알고리즘 자체는 생각보다 단순하다. 일단 0번 노드부터 순차적으로 탐색한다.
이때 자신을 제외한 노드 중 두개의 노드를 택한다. 하나는 출발 노드, 하나는 도착 노드다.
0번 노드를 탐색하는 경우에는 다음과 같이 6가지 경우의 수가 나온다.
(1->2), (1->3), (2->1), (2->3), (3->1), (3->2) // 수학 계산으로는 n-1P2 = (n-1)(n-2) 가지다. (n은 노드의 개수)
그럼 이제 이 각각의 6가지 경우에 대해서 다음을 판단한다.
(1->2)의 경로와 (1->0->2)의 경로 중 더 작은 것은 무슨 경로인가?
즉 지금 탐색 중인 0번 노드를 중간에 껴봐서 둘 중에 누가 더 짧은 경로인지를 비교해보는 것이다.
그래서 더 작은 값으로 테이블을 업데이트한다.
이게 전부다. 이 업데이트를 모든 노드에 대해서 순차적으로 시행해주면 된다.
예를 들면 2->1의 경우 기존에는 테이블[2][1] 값이 '무한'으로 표시되어 있지만 2->0->1을 생각해보면
[2][0]+[0][1] = 5+4=9이다. 더 작은 값이 9이므로 테이블의 [2][1]값이 9로 업데이트 된다.
이게 왜 통하지? 라고 생각할 수도 있는데
다이나믹 프로그래밍 알고리즘을 잘 알고있다면 조금 감이 올지도 모른다. 앞에서 찾아놓은 최단 경로 값을 계속 활용하며 업데이트하기 때문에 최종적으로는 모든 경우에 대한 최단 경로가 잘 구해진다.
- 플로이드 워셜 알고리즘 구현
구현은 더쉽다. 그냥 삼중 반복문을 작성해주면 된다. 위에서는 자신을 제외한 노드 중 두개를 택한다는 얘기를 했지만 이를 고려하지 않아도 최소값을 비교하는 과정에서 알아서 의도대로 돌아간다.
자신을 제외하지 않아도, 또는 출발노드와 도착노드가 동일해도 결국 [i][i]값은 기존의 0이 최솟값일 것이므로 0에서 변하지 않는다.
import sys
inf = sys.maxsize
## number of node: 4, graph is (4x4) matrix... [i,i] is always zero.
graph = [
[0, 4, inf, 6],
[3, 0, 7, inf],
[5, inf, 0, 4],
[inf, inf, 2, 0]
]
def minDist(graph):
result = graph
for i in range(len(graph)):
for j in range(len(graph)): ## j is start point
for k in range(len(graph)): ## k is end point
## update minimum distance if [j->i->k] is shorter than [j->i]
result[j][k] = min(result[j][k], result[j][i]+result[i][k])
return result
print(minDist(graph))
>> [[0, 4, 8, 6], [3, 0, 7, 9], [5, 9, 0, 4], [7, 11, 2, 0]]결과 테이블을 보면 아래의 그림과 같아진다.
(3->1)의 경우를 보자. 그래프를 보며 어림 짐작해보면 3->2->0->1 순서대로 가면 최단경로가 될 거 같다.
이 값은 2+5+4 = 11이다. 테이블을 보니 [3][1]=11이다. 잘 구해졌다.






댓글