https://www.acmicpc.net/problem/17387
17387번: 선분 교차 2
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다.
www.acmicpc.net
x1, y1, x2, y2 = map(int, input().split())
x3, y3, x4, y4 = map(int, input().split())
p1 = [x1, y1]
p2 = [x2, y2]
p3 = [x3, y3]
p4 = [x4, y4]
if min(x1, x2) > max(x3, x4) or min(x3, x4) > max(x1, x2) or \
min(y1, y2) > max(y3, y4) or min(y3, y4) > max(y1, y2):
print(0)
quit()
def ccw(p1, p2, p3):
v1 = [p2[0] - p1[0], p2[1] - p1[1]]
v2 = [p3[0] - p2[0], p3[1] - p2[1]]
return v1[0] * v2[1] - v1[1] * v2[0]
a = ccw(p1, p2, p3) * ccw(p1, p2, p4)
b = ccw(p3, p4, p1) * ccw(p3, p4, p2)
if a <= 0 and b <= 0:
print(1)
else:
print(0)선분 교차 여부를 판정하기 위해 외적이 도입된다.
핵심 아이디어:
p1, p2를 양 끝으로 갖는 선분에 대해 p3, p4에 대해 각각 외적을 해봐서 ccw 여부를 알아낸다. 이때 교차가 되기 위해선는 ccw 결과의 부호가 서로 달라야 한다. 그래야 p3와 p4가 이 선분을 기준으로 반대편에 놓여져 있다고 할 수 있기 때문이다. 마찬가지로 반대 선분에 대해서도 이를 체크하여 똑같이 ccw 부호가 서로 달라야 이 선분들이 교차하고 있다고 말할 수 있다.

위의 아이디어를 기본 원칙으로 하되, 몇몇 예외 상황을 살펴봐야 한다.
상대적인 위치만 보면 되므로 파란 선분 하나를 고정시켜놓고 주황색 선분을 이리저리 움직이며 예외 상황을 살펴보자.



위의 그림과 같이 주황색 선분을 맨 오른쪽에 놓고 돌려가며 여러 상황을 보자. 위의 그림들과 같을 경우, 주황색 선분에 대해 파란 점의 ccw 값은 0이 나오게 된다. 아 그러면 ccw 곱이 음수일 뿐만 아니라 0일 경우에도 교차가 된다고 해주면 되겠구나!! 라고 생각할 수 있지만 또 아래와 같은 예외 상황이 있다.

위와 같은 상황(평행하면서 + 두 선분이 하나의 직선 위에 있으면서 + 만나지 않는 상황)을 미리 배제시켜주기 위해 가장 먼저 다음을 판별해주면 된다.
if min(x1, x2) > max(x3, x4) or min(x3, x4) > max(x1, x2) or \
min(y1, y2) > max(y3, y4) or min(y3, y4) > max(y1, y2):
print(0)
quit()
아래 문제는 좀 더 업그레이드되어 교차점이 1개일 경우 그 좌표까지 구해야 하는 문제다.
https://www.acmicpc.net/problem/20149
20149번: 선분 교차 3
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다.
www.acmicpc.net
x1, y1, x2, y2 = map(int, input().split())
x3, y3, x4, y4 = map(int, input().split())
p1 = [x1, y1]
p2 = [x2, y2]
p3 = [x3, y3]
p4 = [x4, y4]
if min(x1, x2) > max(x3, x4) or min(x3, x4) > max(x1, x2) or \
min(y1, y2) > max(y3, y4) or min(y3, y4) > max(y1, y2):
print(0)
quit()
def ccw(p1, p2, p3):
v1 = [p2[0] - p1[0], p2[1] - p1[1]]
v2 = [p3[0] - p2[0], p3[1] - p2[1]]
return v1[0] * v2[1] - v1[1] * v2[0]
def calc():
# line1
a1 = p2[1] - p1[1]
b1 = p1[0] - p2[0]
c1 = p1[0]*p2[1] - p2[0]*p1[1]
# line2
a2 = p4[1] - p3[1]
b2 = p3[0] - p4[0]
c2 = p3[0] * p4[1] - p4[0] * p3[1]
#intersection point
x = (b2*c1-b1*c2) / (a1*b2-a2*b1)
y = (a2*c1-a1*c2) / (a2*b1-a1*b2)
return [x, y]
a = ccw(p1, p2, p3) * ccw(p1, p2, p4)
b = ccw(p3, p4, p1) * ccw(p3, p4, p2)
if a <= 0 and b <= 0:
print(1)
if (x4 - x3) * (y2 - y1) == (x2 - x1) * (y4 - y3): # 기울기 동일
if max(x1, x2) == min(x3, x4) or max(x3, x4) == min(x1, x2): # 한 점
if p1 in [p3, p4]: print(*p1)
elif p2 in [p3, p4]: print(*p2)
else: print(*calc())
else:
print(0)교차점이 있다고 판단한 경우에 기울기가 같은 경우를 생각해보자. 이 상황에서만 교차점이 여러개 나올 가능성이 있다.
아래의 오른쪽과 같은 경우다.


아래의 코드를 잘 살펴보면 여러 점에서 만나는 상황을 배제한 것을 볼 수 있다.
if (x4 - x3) * (y2 - y1) == (x2 - x1) * (y4 - y3): # 기울기 동일
if max(x1, x2) == min(x3, x4) or max(x3, x4) == min(x1, x2): # 한 점
if p1 in [p3, p4]: print(*p1)
elif p2 in [p3, p4]: print(*p2)
나머지는 수학을 잘 이용해서 교점을 구해주면 된다.
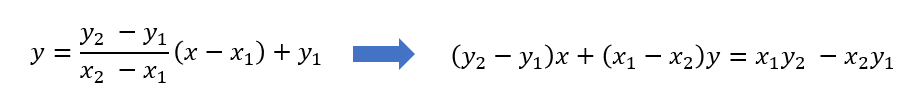



댓글